Viele Tutorien sind so aufgebaut, dass die Befehle, die eine Sprache oder ein Programm beherrscht, der Reihe nach, meist in Gruppen zusammen gefasst, vorgestellt werden, und dann dazu Aufgaben und Fragen gestellt werden, die ein tieferes Verständnis bringen sollen. Bisher ist dieser Text diesem Schema gefolgt, indem zunächst einige grundlegende Dinge erklärt wurden, die zum weiteren Verständnis notwendig sind.
Ab hier soll dann aber ein anderer Weg beschritten werden. Dazu inspiriert wurde ich von dem sehr lesenswerten Buch 'Practical Lisp' von Peter Seibel -- zumindest lesenswert, wenn man sich mit der Sprache Lisp auseinander setzen will (was ich nur wärmstens empfehlen kann).
In diesem Kapitel soll ein vollständiges FORTH-Programm vorgestellt und Schritt für Schritt aufgebaut werden und dabei die Wörter von Forth, die dazu verwendet werden, nur soweit erklärt werden, wie sie zum unmittelbaren Verständnis notwendig sind. Keine Angst! Viele Worte von Forth werden später noch im Detail erklärt, aber hier soll es erst mal darum gehen ein Programm zu schreiben, um ein Gefühl dafür zu bekommen, wie man in Forth programmiert.
Da diese Seite hier ziemlich lang ist und sie vielleicht auch später noch mal das Eine oder Andere nachsehen wollen, ohne direkt wieder die ganze Seite durchsuchen zu müssen, hier eine kleine Navigationshilfe.Jedes Programm beginnt mit einer Idee: "Wäre es nicht schön, wenn mein Computer . . . "
Nun kann man viele Ideen haben, was ein Computer machen soll und wenn man sich in der heutigen Zeit so umschaut und sieht, was Computer so alles leisten, dann kann einen schnell der Mut verlassen, weil man auf die Idee kommt, dass man es nie schafft ein Programm zu schreiben, das in seiner Qualität dahin kommt, dass es mit schon existierenden Programmen konkurrieren könnte.
Das Problem haben wir hier nicht, denn es geht nicht darum ein Programm zu schreiben, das Dinge kann, die bisher keine einzige App auf irgendeinem Smartphone hinbekommt, sondern es geht darum eine Programmiersprache zu lernen. Daher ist es nicht so wichtig, dass dieses Programm schön bunt ist und viel leistet; es kommt viel mehr darauf an, dass die Fähigkeiten und die Charakteristik der Programmiersprache zur Geltung kommen.
Ich habe mich entschieden ein kleines Programm zu schreiben, das einen Bruch kürzt. Sie erinnern sich! Damals, in der Schule! Brüche waren diese Dinger, die keiner leiden konnte und wenn man dann doch damit gerechnet hat, dann hatte der Lehrer sicherlich wieder einen Grund zu meckern und maulte: "Kürzen hättest du das Ergebnis schon noch!" -- Nun, diesen Grund zum Tadel wollen wir ihm nehmen: Unser Programm soll jeden Bruch, den es übergeben bekommt, in gekürzter Form zurück geben.
Ich möchte das Forth-Wort, das es zu programmieren gilt 'TEL' nennen, so dass man eingeben könnte:
4 8 TEL[RETURN] = 1 / 2 ok
Sie erinnern sich daran, dass Forth stackorientiert ist? Wenn ja, dann dürfte ihnen das obige Beispiel keine Probleme machen. Eingegeben werden soll also der Zähler und der Nenner eines Bruchs und dann das Wort 'TEL'. Ausgegeben werden soll dann der gekürzte Bruch, im obigen Beispiel eben Ein halb. Den Programm- (oder Wort-)Namen habe ich natürlich bewusst gewählt, denn mit diesem Namen entspricht das Wort sogar unserer gewohnten Sprechweise. Besteht ein Bruch aus dem Zähler 4 und dem Nenner 8, dann nennen wir das Ganze gerne auch: "Vier Ach tel"
So weit, so gut! Wir wissen, was wir wollen und das ist oftmals schon die halbe Miete. Nun sollte man sich allerdings klar machen, dass gerade bei der Programmierung in Forth oftmals vorher viel Nachdenken gefragt ist, da man sonst ziemlich lange in die blaue Luft programmiert und dann später das Ganze noch mal von vorne anfangen kann. Der erste inhaltliche Abschnitt soll sich daher noch mal mit der Frage beschäftigen, was denn Kürzen eines Bruchs bedeutet.
Ein Bruch ist eine Zahl, die mit zwei Zahlen geschrieben wird, die übereinander stehen und durch einen Bruchstrich getrennt sind. Die obere Zahl nennt man 'Zähler', die untere Zahl 'Nenner'. Der Bruchstrich steht dabei für eine Division.

Wenn man den Zähler und den Nenner eines Bruches mit der gleichen Zahl multipliziert oder sie durch die gleiche Zahl dividiert, ändert sich der Wert des Bruches nicht. Man kann sich das leicht an einem Beispiel klar machen, bei dem die Division, für die der Bruchstrich steht 'aufgeht'.
Wenn der Bruch zum Beispiel den Zähler 8 und den Nenner 2 hat, dann hat der Bruch den Wert 4, denn 8 dividiert durch 2 ist 4. Multipliziert man beide Zahlen z.B. mit 3, dann ist der Zähler 24 und der Nenner 6. Der Wert des Bruches bleibt dabei gleich, denn 24 durch 6 ist immer noch 4. Hätte man statt dessen Zähler und Nenner z.B. durch 2 geteilt, dann wäre der Zähler 4 und der Nenner 1 und der Wert immer noch 4, wie man sich leicht selber klar machen kann.
Die Division von Zähler und Nenner eines Bruches bezeichnet man als kürzen. Das folgende Bild zeigt ein Beispiel:
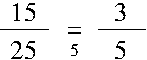
Wie in dem Bild zu sehen, schreibt man gerne die Zahl, durch die der Zähler und der Nenner dividiert wird, unter das Gleichheitszeichen, das die beiden Brüche miteinander verbindet.
Man kann das Kürzen so weit treiben, bis dass es keine Zahl mehr gibt, durch die man den Zähler und den Nenner gleichzeitig teilen kann. Man nennt in einem solchen Fall Zähler und Nenner teilerfremd und den Bruch 'vollständig gekürzt'. Ziel unseres kleinen Programms soll es natürlich sein einen Bruch immer in seiner vollständig gekürzten Fassung zu bekommen. Dazu bieten sich zwei Wege an:
Zugegeben, auch ich habe als Schüler meist die erste Methode angewendet und meist funktioniert sie auch, vor allem dann, wenn man sich daran hält, immer erst die kleinen Zahlen zu probieren und sich langsam zu den größeren vorzuarbeiten.
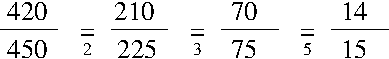
Das Verfahren klappt meistens -- aber eben nur meistens! Wie sieht es aber zum Beispiel mit dem Bruch aus?
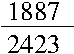
Beide Zahlen, die 1887 und auch die 2423 sind Primzahlen, haben also keine Teiler, aber wenn man das nicht weiß, dann kann man sehr lange rumprobieren, bis man das herausbekommt. Besser ist die zweite Methode, auch wenn sie in vielen Fällen etwas aufwendiger ist: Man bestimmt den ggT.
Jede Zahl lässt sich eindeutig in ihre Primfaktoren zerlegen. Diese Zerlegung findet man am einfachsten, indem man die Zahl erst einmal durch die kleinste Primzahl teilt, durch die sie teilbar ist. Mit dem Ergebnis dieser Division macht man dan weiter, bis es nicht mehr geht; ein Beispiel:
| 420 | Ist teilbar durch 2, also: |
| 2 ⋅ 210 | 210 ist immer noch durch 2 teilbar, also |
| 2 ⋅ 2 ⋅ 105 | 105 ist nicht mehr durch 2, aber durch 3 teilbar: |
| 2 ⋅ 2 ⋅ 3 ⋅ 35 | Bei 35 geht die 5 |
| 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7 | Und das war es! |
Nachdem man entweder den Zähler oder den Nenner so in seine Promfaktoren zerlegt hat, verfährt man mit der jeweils anderen Zahl ebenso.
450 = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 5
Es gibt nun eine ganze Reihe von Verfahren diese Primfaktoren so hinzu schreiben, dass der ggT ablesbar wird, ich bevorzuge die folgende: Zuerst schreibe ich die Primfaktoren der ersten Zahl einfach der Reihe nach in die Zeilen einer Tabelle:
| 420= | 2 | 2 | 3 | 5 | 7 |
| 450= |
Nun werden die Primfaktoren der zweiten Zahl (hier der 450)
ebenfalls in diese Tabelle eingetragen und zwar nach dem folgenden
Verfahren: Man fängt mit dem kleinsten Primfaktor an und trägt ihn
in die Tabelle ein und zwar wenn möglich in eine Spalte, bei der in
der ersten Zeile schon der gleiche Primfaktor steht.
In diesem Beispiel hier wird also die '2' unter die '2' in der
ersten Zeile eintragaen.
| 420= | 2 | 2 | 3 | 5 | 7 |
| 450= | 2 |
Der nächste Primfaktor ist eine '3'. Mit dieser kann noch genau so verfahren werden, also:
| 420= | 2 | 2 | 3 | 5 | 7 |
| 450= | 2 | 3 |
Man achte allerdings darauf, dass ich die '3' nicht einfach in die
nächste Spalte eingetragen habe, sondern eben in die nächste freie
Spalte, bei der in der ersten Zeile schon eine '3' stand.
Nun kommt die zweite '3' und da gibt es dann in der Tabelle keine
entsprechende Spalte mehr, weil in der Zahl 420 die '3' nur einmal
vorkam. In so einem Fall muss eine neue 3er-Spalte angelegt werden,
passenderweise am rechten Ende der Tabelle:
| 420= | 2 | 2 | 3 | 5 | 7 | |
| 450= | 2 | 3 | 3 |
Mit der noch ausstehenden '5' und auch der zweiten '5' verfährt man genauso, so dass die Tabelle am Ende das folgende Aussehen hat:
| 420= | 2 | 2 | 3 | 5 | 7 | ||
| 450= | 2 | 3 | 5 | 3 | 5 |
Betrachtet man nun diese Tabelle, dann gibt es Spalten, bei denen beide Zeilen gefüllt sind:
| 420= | 2 | 2 | 3 | 5 | 7 | ||
| 450= | 2 | 3 | 5 | 3 | 5 |
Es gibt aber auch Spalten, bei denen nur eine Zeile einen Primfaktor enthält:
| 420= | 2 | 2 | 3 | 5 | 7 | ||
| 450= | 2 | 3 | 5 | 3 | 5 |
Um den ggT zu erhalten, muss man nun nur noch die Primfaktoren miteinander multiplizieren, die in einer Spalte stehen, bei der in beiden Zeilen ein Primfaktor steht, hier also:
2 ⋅ 3 ⋅ 5 = 30 = ggT
Das ist dann schon der ggT!
Für diejenigen von ihnen, die noch mehr an Information haben wollen:
Multipliziert man alle vorkommenden Spalten, dann erhält man das
sogenannte kgV, das kleinste gemeinsame Vielfache! Das ist dann der
berühmte 'Hauptnenner', auf den man zwei Brüche erst bringen musste,
bevor man sie addieren oder subtrahieren durfte -- aber das nur
nebenbei!
2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 7 ⋅ 3 ⋅ 5 = 6300 = kgV
Nachdem nun der ggT bekannt ist, kann man den Bruch sofort durch diesen ggT kürzen und erhält den vollständig gekürzten Bruch. (Für das 'richtige' Leben sei noch folgendes gesagt: Man braucht eigentlich die beiden Zahlen gar nicht durch den ggT zu teilen, weil man der Tabelle sofort das Ergebnis dieser Division ansehen kann, aber das wäre dann doch ein bisschen viel Mathematik und ghört nicht hier hin. Wenn es sie interessiert, dann sehen sie sich mal die letzte Tabelle und den vollständig gekürzten Zähler und Nenner an, vielleicht fällt es ihnen ja selber auf, was es damit auf sich hat.
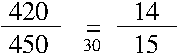
So! Der erste Schritt ist getan! Nun wissen wir schon ziemlich genau, was wir eigentlich wollen, wenn wir ein Program schreiben wollen, dass einen Bruch vollständig kürzt. Der Vollständigkeit halber sei das Ganze aber noch einmal in einer Liste aufgeführt:
Jeden dieser Schritte haben wir oben an einem Beispiel auch schon ausprobiert. Das soll nun in einem Programm nachformuliert werden. Das ist übrigens guter Programmierstil! Zuerst überlegen, was man eigentlich genau haben will und dann erst mir der eigentlichen Programmierung beginnen.
Nun soll es also losgehen mit dem ersten kleinen Stück Programm! Aber womit sollte man am besten anfangen? Charles H. Moore, der Erfinder von Forth wies einmal darauf hin, dass es in Forth absolut guter Stil ist, die einzelnen Wortdefinitionen, die nachher das Programm ausmachen, möglichst klein zu halten und weiterhin darauf zu achten, dass man möglichst Worte definiert, die man auch in einem anderen Zusammenhang vielleicht noch brauchen kann.
Eine solche kleine Einheit, die uns dienlich sein wird, und die man auch im anderen Zusammenhang brauchen kann, ist ein Wort, das uns entscheiden hilft, ob eine Zahl Teiler einer anderen Zahl ist, oder eben nicht. Mit diesem Wort werden wir später dann testen, ob ein bestimmter Primfaktor in einer der beiden Zahlen, Zähler und Nenner, enthalten ist, oder nicht.
Auch hier besteht nun der erste Schritt darin, sich genau zu überlegen, was das Wort denn können soll und vor allem, wie es arbeiten soll. Am besten überlegt man sich daher erst mal den Aufruf dieses Wortes. Ich halte es für sinnvoll, wenn man es folgendermaßen aufrufen kann:
Zahl Teiler ?HAT-TEILER
Entsprechend der Regeln für UPN, die ich früher schon beschrieben habe, entspricht dieser Aufruf einer Infix-Notation, die dann ungefähr folgendermßen aussähe:
Zahl ?HAT-TEILER Teiler
Das Fragezeichen im Wortnamen deutet dabei an, dass es sich um einen Test handelt.
Nun kommt der zweite Schritt: Was soll das Wort liefern? Hier sind zwei Möglichkeiten denkbar, je nachdem, ob 'Teiler' auch wirklich ein Teiler der 'Zahl' ist oder nicht. Außerdem sollte man sich Gedanken darüber machen, in welcher Reihenfolge die Werte denn auf dem Stack vom Wort zurück gelassen werden sollten. Mit anderen Worten: Man sollte sich Gedanken über den Stack machen. Sinnvoll wären die folgenden Möglichkeiten:
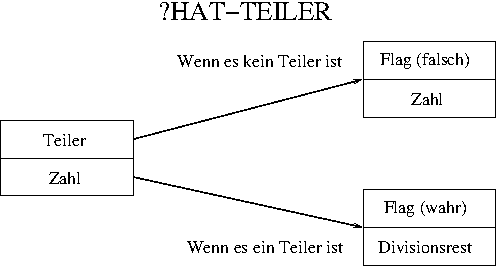
Dieses Bild bedarf ein Wenig der Erläuterung! Zum einen ist zu sehen, dass es zwei Möglichkeiten gibt, eine für den Fall, das der 'Teiler' kein Teiler der Zahl ist und eine, im Bild unten dargestellte, für den Fall, dass sie ein Teiler ist.
Die meisten Begriffe im Bild dürften klar sein, aber bevor ich zu der Reihenfolge auf dem Stack komme, noch ein Wort zu 'Flag', was im Bild auftaucht. In anderen Programmiersprachen nennt man so etwas auch gerne eine boolschen Wert, also einen Wert, der nur die beiden Werte 'falsch' oder 'wahr' annehmen kann. In Forth heißt so etwas eben Flag, aber ansonsten ist Forth nicht viel anders, als andere Programmiersprachen auch. Der (Zahl)Wert Null wird als 'falsch' interpretiert und alle anderen Zahlwerte als 'wahr'. Unser Wort sollte also als Wahrheitswert eine Zahl ausgeben, die 0 ist, wenn 'Teiler' kein Teiler der Zahl ist und einen anderen Wert haben, wenn sie Teiler ist.
Nun noch ein Wort zu der Reihenfolge auf dem Stack. Wie im Bild zu sehen, befindet sich oben auf dem Stackstapel der Teiler oder eins der beiden Flags und die Zahl, beziehungsweise der Divisionsrest darunter. Wieso ist das so gewählt und nicht anders herum. Für die Eingabe habe ich das oben schon erklärt, denn es entspricht der Umsetzung der UPN-Schreibweise in unsere, vielleicht gewohntere Infix-Schreibweise, aber wieso die Ausgabe?
Nun, das ist schnell erklärt: Nach Aufruf des Wortes interessiert uns zuerst, ob der 'Teiler' auch wirklich Teiler war, daher sollte das Flag oben liegen. Wenn wir es interpretiert und damit vom Stack entfernt haben, dann sollte man es entweder mit einer anderen Zahl probieren, dann braucht nur die auf den Stack gelegt zu werden, weil die ursprüngliche Zahl ja noch da liegt. Ist der 'Teiler' allerdings wirklich ein Teiler der Zahl, dann braucht man die Zahl eigentlich nicht mehr sondern hätte lieber schon das Divisionsergebnis. Wenn man sich oben noch mal ansieht, wie man eine Zahl in Promfaktoren zerlegt, wird klar, was ich meine.
In Forth gibt es nun ein Wort, welches unseren Bedürfnissen perfekt
angepasst zu sein scheint (und wie wir sehen werden, auch ist);
/MOD! Was macht dieses Wort? Nun, es erwartet zwei
Zahlen auf dem Stack und dividiert die erste durch die zweite.
Allerdings erfolgt diese Division auf eine ganz besondere Art, eine
Art, die sie vielleicht noch aus der Grundschule her kennen. Damals
kannten sie nur ganze Zahlen, also keine Brüche und keine
Dezimalzahlen. Daher ergab eine Division zum Beispiel:
14 durch 3 gleich 4 Rest 2
Damit war gemeint, dass die 3 viermal 'in die 14 hineingeht' und
dann noch ein Rest von 2 übrig bleibt. Genau so, wie das damals in
der Grundschule gemacht wurde, macht es nun auch /MOD.
Spielen wir mal ein bisschen damit rum:
14 3 /MOD OK . 4 OK . 2 OK
Betrachten wir das Ergebnis unserer kleinen Spielerei: Zuerst wurden
die Zahlen 14 und 3 auf den Stack gebracht, die 14 unten und
zuoberst die 3, da sie erst danach angegeben wurde. Dann wurde
/MOD aufgerufen und dann lagen wieder zwei Zahlen auf
dem Stack, zuoberst die 4, die mit dem ersten Punktwort vom Stack
geholt und ausgegeben wurde, und darunter die 2, der Divisionsrest.
Ein weiteres Beispiel:
531 31 /MOD OK . 17 OK . 4 OK
Eine kleine Überlegung zeigt, dass auch hier alles seine Ordnung hat, denn 531 durch 31 ist 17 Rest 4! Um zu testen, ob eine Zahl Teiler einer anderen ist, ist das Wort perfekt geeignet. Betrachten sie folgendes Beispiel:
15 3 /MOD OK . 5 OK . 0 OK
Wenn eine Zahl Teiler der anderen ist, dann ist das Ergebnis schon fast das, was wir haben wollten, allerdings in falscher Reihenfolge, denn das Flag sollte ja oben auf dem Stack liegen und außerdem ist es das 'falsche' Flag, denn in dem obigen Beispiel ist ja die 3 ein Teiler von 15 und daher sollte das Flag gerade etwas anderes sein, als 0.
Noch schlechter sieht die Sache aus, wenn man sich den Fall überlegt, dass die Zahl kein Teiler der Zahl ist. Dann liegt zwar ein (unbrauchbares) Divisionsergebnis vor, aber der Divisionsrest ist dann auch wieder ein 'falsches' Flag und vor allem ist die ursprüngliche Zahl nicht mehr da, die ja in einem solchen Falle mit ausgegeben werden sollte. Was tun sprach Zeus zu seinen Göttern?
Bisher war immer nur vom Stack die Rede und dass Forth diesen Stack nutzt, um Daten an ein Wort zu übergeben oder es von ihm zurück zu bekommen. Das mancht allerdings nur dann Sinn, wenn man auf diesen Stack auch zugreifen und ihn verändern kann. Und das kann Forth!
Sehen wir uns die Probleme an und gehen sie an. Im letzten Abschnitt
wurde ja schon deutlich, dass insbesondere zwei Probleme auftreten.
Nach der Verwendung von /MOD liegt die ursprüngliche
Zahl nicht mehr auf dem Stack, obwohl sie unter Umständen noch mal
gebraucht wird. Man sollte sie dazu 'verdoppeln', was hier besonders
gut mit dem Wort OVER funktioniert.
OVER erwartet zwei Zahlen auf dem Stack und kopiert die
zweite Zahl auf dem Stack nach oben an die (dann) oberste Stelle. Am
einfachsten mancht man sich das mit einem Bild klar:
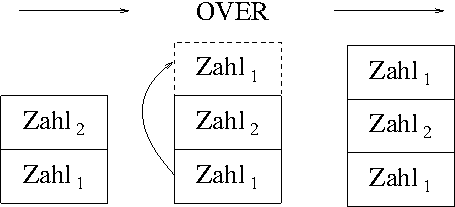
Wenden wir OVER auf unser Beispiel an, dann ist das
Ergebnis schon akzeptabel. Nach OVER sieht der Stack
folgendermaßen aus:
| Zahl | Teiler | Zahl |
Die Zahl ist schon mal verdoppelt, allerdings liegen nun Zahl und
Teiler 'verkehrt' herum auf dem Stack, jedenfalls aus der Sicht von
/MOD; Kein Problem! Da hilft das Wort
SWAP, der einfach die beiden obersten Zahlen auf dem
Stack tauscht.
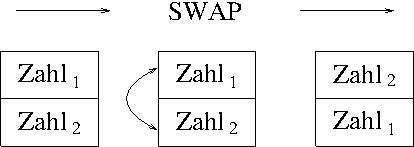
Nun sollen die drei Wörter mal hintereinander ausgeführt werden und dabei der Stack im Auge gehalten werden:
Wörter:
| |
OVER |
SWAP |
/MOD |
| |||||||||||
Stack:
|
|
|
|
|
|
Das ist eigentlich genau das, was wir brauchen. Alle Werte, die im Ergebnis vorkommen können, liegen nun vor: Die Zahl, die wir brauchen, wenn die Division nicht aufging, den Quotient, wenn sie aufging und den Divisionsrest, der als Flag interpretiert werden kann; letzterer allerdings immer noch 'falsch', aber darum kümmern wir uns später.
Nachdem wir soweit sind, kommen wir zur Entscheidung, ob die
Division erfolgreich war, oder nicht. Dazu wird das Flag gebraucht,
das wir mit OVER nach oben holen. Dass es nun zweimal
auf dem Stack liegt, interessiert uns nicht weiter, denn die
Entscheidungsworte in Forth 'fressen' ein Flag, da wir es auch
noch zurückgeben wollen, ist es sogar gut, dass es doppelt vorliegt.
Das Wort, der uns nun weiter hilft ist IF.
IF ist der einfachste das Entscheidungswort in
Forth. Er kommt in zwei Varianten vor, einmal:
IF ... THEN
In diesem Fall nimmt IF die oberste Zahl vom Stack und
interpretiert sie als Flag. Ist es war, also die Zahl nicht Null,
dann wird einfach hinter dem IF weiter gemacht und das
THEN ignoriert. Ist das Flag allerdings Null, wird also
als falsch interpretiert, dann wird die Ausführung sofort hinter dem
THEN weiter geführt und der Teil zwischen
IF und THEN ausgelassen.
Gerade Anfänger tun sich mit der Benennung etwas schwer, vor allem,
wenn sie vorher andere Programmiersprachen gewohnt waren. Das
THEN in Forth entspricht in anderen Sprachen eher einem
endif, also der Beendigung einer bedingten
Programmausführung. Die zweite Form von IF ist:
IF ... ELSE ... THEN
Auch hier wertet IF die oberste Zahl auf dem Stack als
Flag aus. Ist dieses Flag wahr, dann wird auch wieder der Teil
hinter dem IF ausgeführt, allerdings nicht bis zum
THEN, sondern nur bis zum ELSE. Wird
ELSE erreicht, geht die Bearbeitung hinter dem
THEN weiter. Ist das Flag falsch, dann wird der Teil
zwischen IF und ELSE ausgelassen und der
Teil zwischen ELSE und THEN abgearbeitet
und danach hinter dem THEN weiter gemacht.
Man kann vereinfachend sagen, dass der Teil zwischen IF
und ELSE der Wahrheitsteil des Programms ist und
der Teil zwischen ELSE und THEN der
Falschheitsteil.
Da wir die Inhalte auf dem Stack in jedem Fall umbauen müssen, also
unabhängig davon, ob die Division eine Rest ließ oder nicht,
brauchen wir das IF-Wort in der zweiten Form. Der
Stack sind dann in beiden Teilen, also zwischen dem IF
und dem ELSE und auch zwischen ELSE und
THEN gleich aus:
| Quotient |
| Rest |
| Zahl |
Betrachten wir erst mal den Teil, wenn die Division nicht aufging,
also ein Rest übrig blieb. Damit landen wird zwischen
IF und ELSE. Dort muss sicher gestellt
werden, dass der Quotient verschwindet, da er nicht mehr gebraucht
wird. Das erledigt ein einfaches Wort: DROP.
DROP ist sehr einfach: Dieses Wort
entfernt einfach die oberste Zahl vom Stack.
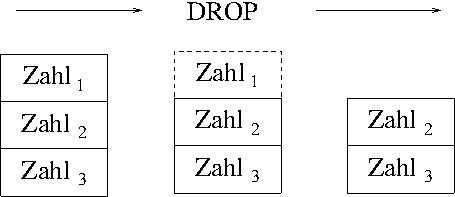
Wie wir gleich sehen werden, war es das für diesen Teil schon.
Wenden wir uns dem Teil zu, der zwischen ELSE und
THEN steht, also der, der ausgeführt wird, wenn die
Division ausging und daher der Rest Null war. Hier hilft ein anderes
Wort: ROT. ROT holt den drittobersten
Eintrag auf dem Stack an die oberste Stelle. Er kopiert ihn nicht,
wie es OVER tat, sondern er verschiebt ihn.
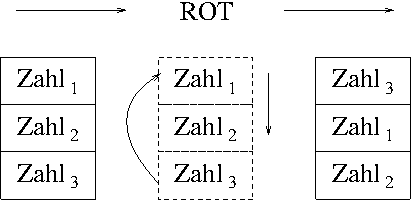
Mit ROT holen wir die nun nicht mehr benötigte Zahl
nach oben auf den Stack, wo wir sie mit DROP
'vernichten' können. Wenn wir nun noch Quotient und Rest mit
SWAP vertauschen, sind wir fast fertig.
Nach dem 'Wahrheitsteil' von IF liegt nun das
(allerdings immer noch 'falsche') Flag oben auf dem Stack und
darunter die Zahl. Nach dem 'Falschheitsteil' oben das falsche Flag
und darunter der Quotient. Eigentlich muss nur noch aus dem
'falschen' Flag ein richtiges gemacht werden und das geht mit
0=.
Das Wort 0= macht eigentlich das, was sein Name schon
sagt, er testet die oberste Zahl auf dem Stack daraufhin, ob sie
Null ist oder nicht. Wenn es eine Null ist, dann wird 'wahr' auf dem
Stack hinterlegt, ist es keine Null, dann wird 'falsch' auf dem
Stack hinterlegt. Es findet also gerade ein Austausch von 'wahr' und
'falsch' bzw. 'Null' und 'Nicht-Null' statt, den wir hier brauchen
können.
Tja, das war es schon. Alles, was zu tun übrig bleibt, ist es das neue Wort zu definieren und das ist sehr einfach:
: ?HAT-TEILER OVER SWAP /MOD OVER IF DROP ELSE ROT DROP SWAP THEN 0= ;
Eine kleine Bemerkung an diejenigen, die schon Erfahrung mit anderen Programiersprachen haben: Die gesamte Wortdefinition hat gerade mal 70 Zeichen wovon 11 alleine für den Namen des neuen Wortes gebraucht werden. Trotzdem ist der Kode lesbar, denn die verwendeten Forth-Worte sind allemale leicht zu merken, wenn man erst mal eine Weile damit gearbeitet hat. Versuchen sie das ruhig mal in ihrer Programmiersprache. Aber das ist noch nicht alles: Im Speicher 'verbraucht' das neue Wort gerade mal 100 Byte und das auch nur, weil ich es in einem 32-Bit Forth geschrieben habe; bei klassischen 16-Bit Forthversionen wäre es dort noch kleiner!
Der Weg bis hier war lang! Ich verspreche ihnen, dass es ab jetzt etwas zügiger geht, aber einige Aspekte waren einfach nötig: Zum einen haben sie bis hier schon einige Forth-Worte kennen gelernt, und sich haben auch gelernt, wie man in Forth Probleme angeht. Außerdem haben sie gesehen, wie man in Forth mit dem Stack umgeht, auch wenn das nicht bis ins Detail gegangen ist. Als letztes wissen sie nun auch schon, wie in Forth Entscheidungen realisiert werden.
Der nun folgende Schritt behandelt die Frage, wie man eine Zahl in ihre Primfaktoren zerlegt. Aus Gründen, die ich hier noch nicht erklären kann, soll ein erstes Modell dieses Wortes eine Zahl übergeben bekommen und diese dann in Primfaktoren zerlegen, die einfach nur ausgegeben werden. Das Problem die Primfaktoren in eine Tabelle einzutragen, wird später behandelt. Es dürfte also klar sein, dass wir etwas wollen wie:
420 PRIMF 2 2 3 5 7 ok
Über wohl kein Problem in der Mathematik ist mehr nachgedacht worden, als über die Frage, wie man Primzahlen berechnet oder eine Zahl in ihre Primfaktoren zerlegt. Da es hier nicht darum geht ein neues, geniales Primzahlprogramm zu schreiben, kann man das ganze recht einfach erledigen, auch wenn die Routine ziemlich uneffizient ist:
Wie auch gerade sollte man sich zunächst Gedanken über den Stackverlauf machen. Zu Beginn liegt da nur die Zahl, die zerlegt werden soll, aber es wird ja als aller erstes die 2 als möglicher Teiler hinzugefügt. Damit sieht der Stack folgendermaßen aus:
| Mögl. Teiler |
| Zahl |
Unser Testwort ?HAT-TEILER belässt einen möglichen
Teiler ja nicht auf dem Stack, daher muss dieser gerettet werden,
ein einfaches SWAP OVER leistet das. Danach hat unser
Stack die Form:
| Mögl. Teiler |
| Zahl |
| Mögl. Teiler |
Nun kommt unser Wort ?HAT-TEILER. Danach hat der Stack
zwei mögliche Formen:
| Flag falsch |
| Zahl |
| Mögl. Teiler |
oder
| Flag wahr |
| Quotient |
| Mögl. Teiler |
Das oben liegende Flag kann sofort für eine Entscheidung genutzt
werden. Im wahren Teil muss der Teiler ausgegeben werden. Dazu
werden die beiden Werte getauscht und der dann oben liegende Teiler
verdoppelt. Das geschieht mit dem Wort DUP.
War das Ergebnis falsch, dann müssen die Einträge auf dem Stack
wieder getauscht und der mögliche Teiler um Eins erhöht werden. Das
geschieht mit 1+
Nach der Entscheidung muss noch geprüft werden, ob der Quotient den Wert 1 erreicht hat. Ist das der Fall, kann das Wort beendet werden, ansonsten muss wieder beim Divisionsversuch weiter gemacht werden.
Alles, was man jetzt noch wissen muss ist, wie in Forth eine
Schleife realisiert werden kann. Es gibt mehrere Möglichkeiten, hier
ist die zweckmäßigste die Schleife, die mit BEGIN ...
UNTIL gebildet wird. Die beiden Worte können nur in einer
Doppelpunktdefinition verwendet werden. Zunächst werden die Worte
hinter BEGIN ausgeführt, bis das Wort
UNTIL erreicht wird. Dieses interpretiert die oberste
Zahl auf dem Stack als Flag. Ist das Flag 'wahr', dann werden als
weiteres die Worte hinter UNTIL ausgeführt. Ist es
'falsch', dann werden die Worte hinter BEGIN erneut
ausgeführt.
Die Definition unseres neuen Wortes sieht nun folgendermaßen aus:
: PRIMF 2 BEGIN SWAP OVER ?HAT-TEILER
IF SWAP DUP . ELSE SWAP 1+ THEN
OVER 1 = UNTIL DROP DROP ;
Nur zwei Dinge dürften vielleicht noch unklar sein. Zum einen das
doppelte Wort DROP am Ende des Wortes. Sie sind
leicht zu erklären, denn nachdem die Schleife verlassen wird, liegen
ja immer noch der letzte Teiler und die 1 als Divisionsrest auf dem
Stack, da wir unsere Umgebung 'sauber' verlassen wollen und der
Stack nach Aufruf des Wortes leer sein sollte, werden diese beiden
Werte einfach gelöscht.
Das zweite ist die Kombination 1 = kurz vor dem
UNTIL. Die 1 wird zu dem Divisionsergebnis, das zu
diesem Zeitpunkt oben auf dem Stack liegt hinzugefügt. Das
Forth-Wort = nimmt die obersten zwei Werte vom Stack
und prüft, ob sie gleich sind. Zurück gegeben wird dann ein Flag,
das von UNTIL ausgewertet wird.
Außerdem sollte man daran denken, dass diese Wortdefinition nur vorläufig ist. Später wäre eine sinnvoller, bei der die Primfaktoren auf dem Stack zurück gelassen werden.
So langsam nähern wir uns der Möglichkeit den ggT von Zähler und Nenner des Bruchs bestimmen zu können. Genauer gesagt haben wir die Möglichkeit schon. Man könnte ja einfach mit der kleineren der beiden Zahlen beginnen und von da an abwärts testen, bis eine Zahl gefunden wird, die Teiler von beiden Ausgangszahlen ist.
Ich möchte hier aber einen anderen Weg einschlagen. Zum einen möchte ich möglichst nahe am oben beschriebenen Vorgehen bleiben und zum anderen will ich ihnen noch eine phantastische Möglichkeit von Forth präsentieren, die bei der oben vorgeschlagenen Variante nicht erforderlich ist. Außerdem hat diese Variante den Nachteil, dass der ggT eigentlich durch 'Ausprobieren' ermittelt wird -- kein wirklich eleganter Weg.
Worum geht es? Das Problem liegt in der Tabelle, und der Frage, wie man eine solche Tabelle in Forth anlegt.
Neulinge in Forth, die schon Erfahrungen mit anderen
Programmiersprachen gemacht haben, sind in der Regel erstaunt, dass
es in Forth kaum Möglichkeiten gibt Variablentypen anzugeben und
schon gar keine strukturierten Datentypen. Es gibt keine Arrays,
keine Strukturen oder Ähnliches, was man aus anderen
Programmiersprachen kennt. Es gibt eigentlich nur ein einziges Wort,
nämlich VARIABLE, mit dem eine Variable angelegt werden
kann. Und dieses Wort erlaubt es auch nur eine Variable für eine
Ganzzahl zu erzeugen, wirkich kein Grund zum Jubeln.
Ein klein wenig versöhnt das Wort ALLOT. Mit diesem
Wort ist es möglich den Platz, den VARIABLE zugewiesen
bekommt, zu vergrößern, aber immer noch nicht das gelbe vom Ei.
Es gibt in Forth keine strukturierten Datentypen, man kann sie sich aber machen! Und das ist der eigentliche Witz von Forth. In Sprachen, wie C gibt es bestimmte Datentypen, wie 'int', 'float', 'char'. Mit geeigneten Sprachbestandteilen kann man sie zu Arrays oder Strukturen kombinieren, die dann eine gewissen logische Einheit bilden. Das ist einerseits komfortabel, andererseits ist es unflexibel, denn auch wenn es einige Typen gibt, gibt es eben auch nur diese Typen und ein Programmierer in dieser Sprache muss sich darum kümmern, wie er seine Aufgabe im Rahmen dieser Datentypen darstellen kann. So gibt es in manchen Pascalderivaten den Datentyp 'boolean', der die Werte 'true' und 'false' annehmen kann. In C gibt es einen solchen Datentyp nicht und wenn man in C mit diesem Datentyp programmieren will, dann muss man sich behelfen, indem man z.B. den Datentyp 'char' in gewisser Weise interpretiert.
Ganz anders in Forth. Hier hat man die Möglichkeit seine eigenen Datentypen zu schaffen. So wäre es sehr einfach in Forth einen Datentyp 'boolean' zu erzeugen. Man kann also den Kompiler tatsächlich seinen Bedürfnissen anpassen! -- Die sicherlich stärkste Möglichkeit von Forth.
Bevor es nun lustig daran geht einen Datentyp zu schaffen, mit dem das Problem des ggT gelöst werden kann, muss noch eine kleine Vorüberlegung erfolgen. Ich werde dieses Thema in einem späteren Kapitel noch einmal vollständiger erörtern, hier soll es nur darum gehen die Grundbegriffe zu verstehen.
Der wichtigste Aspekt, der bei den folgenden Überlegungen eine Rolle spielt ist das Begriffspaar Laufzeit -- Kompilierzeit. Was ist damit gemeint?
In den meisten Programmiersprachen haben Wörter eine bestimmte Bedeutung und das war es. In C zum Beispiel bedeutet '=', dass der Seite links von diesem Zeichen der Wert, der rechts von diesem Zeichen steht zugewiesen wird. In Forth ist das anders, da haben Wörter zwei Bedeutungen. Im Regelfall fällt das gar nicht auf, aber der Unterschied zwischen der Bedeutung, wenn ein Wort kompiliert wird und dem, wenn das Wort aufgerufen wird, ist wesentlich und soll daher verdeutlicht werden.
Betrachtet man z.B. das Wort .", dann scheint seine
Aufgabe darin zu liegen alles bis zum nächsten Anführungszeichen auf
dem Bildschirm auszugeben. Aber man betrachte den folgenden
Ausschnitt aus einer Forth-Sitzung (Um besser darauf Bezug nehmen zu
können, habe ich Zeilennummern vor die einzelnen Zeilen geschrieben:
[1] ." Hallo" [2] Hallo OK [3] : sag-hallo ." Hallo" ; [4] OK [5] sag-hallo [6] Hallo OK
In diesen sechs Zeilen wird das Wort ." dreimal
verwendet, zweimal direkt und einmal indirekt. In Zeile [1] und in
Zeile [3] taucht es direkt auf und in der Zeile [5], in der
sag-hallo aufgerufen wird, wird es indirekt aufgerufen,
da es ja Bestandteil von sag-hallo geworden ist.
Außerdem kann man es auch daran erkennen, dass
sag-hallo ja auch 'Hallo' ausgibt (in Zeile [6]).
In Zeile [1] und in Zeile [5] macht ." auch das, was es
tun soll, es gibt 'Hallo' aus. In Zeile [3] wird ."
zwar verwendet, gibt aber kein 'Hallo' aus.
In Zeile [3] wird ." innerhalb einer
Doppelpunktdefintion verwendet. Das 'normale' Verhalten von
." wird in die neue Definition von
sag-hallo kompiliert, was nichts anderes bedeutet, dass
sag-hallo, wenn es aufgerufen wird, Text auf dem
Bildschirm ausgibt. Dazu bringt ." irgendwie den Text,
der später von sag-hallo ausgegeben werden soll in der
Definition von sag-hallo unter und außerdem auch noch
das, was später mit diesem Text geschehen soll, wenn
sag-hallo aufgerufen wird. Dieses Verhalten von
." nennt man sein
Kompilierzeitverhalten.
Das 'normale' Verhalten von .", nämlich Text auf dem
Bildschirm auszugeben, nennt man sein
Laufzeitverhalten.
Vereinfacht kann man sagen, dass das Laufzeitverhalten das ist, was ein Wort macht, wenn es aufgerufen wird und das Kompilierzeitverhalten das, was es macht, wenn damit ein neues Wort 'erzeugt' werden soll.
Es gibt nun eine ganze Reihe von Worten, mit denen man neue Worte
definieren kann. Einige davon kennen sie bereits: : ist
das bekannteste, VARIABLE haben sie zumindest schon mal
rudimentär kennen gelernt. Hier soll nun gezeigt werden, wie man ein
neues Wort definiert, mit dem man neue Worte definieren kann, die
dann gemeinsame Eigenschaften haben. Die beiden Zauberwörter heißen
CREATE und DOES>.
Ich gebe zu, die Formulierung: "...ein Wort, mit dem man neue Worte definieren kann..." ist schon ziemlich kryptisch. Ich gehe daher den Weg, den ich schon das ganze Kapitel hindurch verfolge: Ich mache es mit einem Beispiel und zwar einem, das zu unserer Problematik mit dem ggT passt.
Bisher ist ja noch unklar, wie die Primfaktoren gespeichert werden sollen aus denen dann der ggT berechnet werden kann. Es bietet sich ein zweidimensionales Array an. Das heißt eine Art Tabelle mit zwei Zeilen und einer ausreichenden Anzahl von Spalten in welche die Primfaktoren eingetragen werden können.
In einem ersten Schritt wird nun ein Wort definiert mit dem man dann zweizeilige Tabellen erzeugen kann und das festlegt, wie diese Tabellen zur Laufzeit denn arbeiten sollen. Dazu ist es jetzt sinnvoll sich noch einmal Gedanken über Computerspeicher zu machen. Ich habe im vorigen Kapitel dargelegt, dass Computerspeicher aus intereinander liegenden Speicherstellen besteht, die von Forth in Zellen unterteilt werden. Der Knackpunkt ist, dass sie hintereinander liegen und eben nicht zweidimensional angeordnet sind. Man muss sich also was einfallen lassen. Ein einfacher Ansatz ist der folgende:
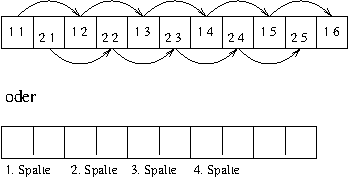
Die (hier) hintereinander liegenden Speicherzellen werden abwechselnd der erste und der zweiten Zeile der Tabelle zugeordnet. Das ist erkennbar an den Indizes, die ich in die Speicherzellen hineingezeichnet habe. Der erste Index gibt immer die Zeilen- der zweite die Spaltennummer an.
Unser neues Definitionswort, mit dem dann eine neue Arrayvariable (oder eben Tabellenvariable) erzeugt werden kann, soll eine Zahl übergeben bekommen und die entsprechende Anzahl von Spalten erzeugen. Schauen wir uns den Beginn derDefinition dieses Wortes einfach mal an.
: MACH-TABELLE CREATE 8 * ALLOT ...
Das Wort MACH-TABELLE soll zuerst einen neuen Eintrag
erzeugen (das geschieht mit CREATE) und dann das
Achtfache der Zahl auf dem Stack als Speicher reservieren (das
passiert mit dem ALLOT). Wenn man es also zum Beispiel
folgendermaßen aufruft:
20 MACH-TABELLE FRITZ ...
Dann wird eine Tabelle erzeugt, die den Namen 'FRITZ' erhält und die Platz für 20 Spalten hat. Diese Definition basiert auf der Annahme, dass eine Zelle 4 Byte beansprucht. Da für jede Spalte zwei Zellen angelegt werden sollen, muss die Anzahl der Bytes berechnet werden, indem die Anzahl der gewünschten Spalten mit 8 multipliziert werden. Das ist für die Kompilierzeit schon alles. Nun kommt der Defintionsteil, der von dem neuen Wort (im obigen Beispiel 'FRITZ') ausgeführt werden soll, wenn es aufgerufen wird. Sinnvoll wäre in unserem Zusammenhang sicherlich ein Aufruf der Form:
13 FRITZ
Es ist ein Leichtes in Forth eine Variablendefinition anzulegen, bei
der sowohl die Zeile als auch die Spalte angegeben wird. Für unser
Problem ist es aber sinnvoller und einfacher, wenn nur die
Spaltennummer angegeben wird. Damit ist mit dem obigen gemeint, dass
FRITZ zur Laufzeit die Adresse der 13ten Spalte zurück
geben soll. Die Kodierung ist eigentlich recht simpel:
: MACH-TABELLE CREATE 8 * ALLOT DOES> SWAP 8 * + ;
Hinter dem DOES> geht es los, wobei DOES>
die Adresse der ersten Speicherzelle auf den Stack legt. Nun muss
nur noch die Nummer der Spalte (Die Zählung der Spalten beginnt mit
0!) mit 8 multipliziert werden und das Ergebnis zur obigen Adresse
addiert werden, um die Adresse der entsprechenden Spalte zu
erhalten. Adresse und Spaltenzahl werden dazu vertauscht, damit die
Spaltenzahl und nicht die Adresse mit 8 multipliziert wird. Das ist
der Laufzeitkode jedes Arrays, den wir haben wollen. Das Ganze noch
mal im Überblick:
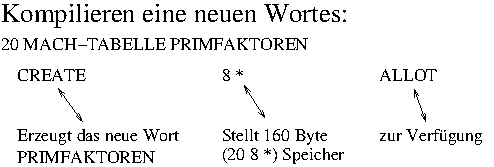
Und nun, was passiert, wenn man das neue Wort
PRIMFAKTOREN aufruft (mit zwei Werten auf dem Stack)

Der Weg bis hier war lang! Aber nun werden sie auch sehen, dass es wirklich nicht mehr schwer ist das ursprüngliche Problem mit dem gekürzten Burch zu lösen.
Als erstes sollte nun eine Variable erzeugt werden, welche die Primfaktoren aufnimmt. Hier muss eine Entscheidung getroffen werden. So, wie das Ganze bisher aufgesetzt ist, muss die Anzahl der Primfaktoren begrenzt werden. Ein sinnvoller Wert ist sicherlich die 50, da Brüche mit mehr als 50 Primfaktoren treten doch eher selten auf (Man kann das Problem aber natürlich auch so lösen, dass man einen anderen Variablentyp erfindet, der beliebig erweitert werden kann, aber das würde hier zu weit führen). Somit definieren wir:
50 MACH-TABELLE PRIMFAKTOREN
MACH-TABELLE stellt zwar Speicher bereit, aber wir
wissen nicht, was in diesem Speicher steht. Es ist denkbar, dass
hier noch Inhalte von früheren Aktivitäten stehen. Man sollte daher
ein Wort 'erfinden', mit dem die Tabelle geleert werden kann. Das
geht einfach mit dem Wort FILL. FILL
bekommt eine Adresse, eine Anzahl von Bytes und einen Wert übergeben
und füllt dann ab der Adresse die Anzahl von angegebenen Bytes mit
dem Wert. Um die Tabelle zu leeren, reicht daher:
: LEER 0 PRIMFAKTOREN 50 8 * 0 FILL ;
Nun geht es daran den Kode zu schreiben, mit dem die Tabelle gefüllt wird. Wie oben beschrieben werden dazu zwei Methoden verwendet. Bei beiden ist es aber so, dass eine Zahl immer nur in die Tabelle eingetragen wird, wenn dort eine Null steht. Es ist daher sinnvoll ein Wort zu definieren, das die nächste Adresse findet, bei der eine Null gespeichert ist.
: NAECHSTE0 BEGIN DUP @ WHILE 8 + REPEAT ;
Eine Schleife der Form BEGIN ... WHILE ... REPEAT wird
so lange durchlaufen, solange die getestete Bedingung vor
WHILE wahr ist. Da jeder Wert, der nicht Null ist, als
wahr interpretiert wird, reicht es den Inhalt der Speicherstelle so
zu testen. Wird eine Null gefunden, dann bricht die Schleife ab,
sonst einfach eine 8 zur letzten Adresse addiert.
Es gibt zwei Füllmethoden, die erste ist einfach:
: FUELL 0 PRIMFAKTOREN NACHSTE0 ! ;
Übergeben wird ein Primfaktor. Ausgehend von der ersten Spalte und der ersten Zeile wird der erste Eintrag in der Tabelle gesucht, der Null ist und der Wert dort eingetragen.
Bei der zweiten Methode wird es etwas komplizierter. Als erstes muss der Anfang der zweiten Zeile gefunden werden, was einfach dadurch passiert, dass 4 zur Anfangsadresse der ersten Spalte addiert wird. Von da aus wird immer die nächste Spalte mit dem Wert Null gesucht und der Wert dann eingetragen, wenn in der ersten Zeile eine Null oder die gleiche Zahl steht. Das ist schon ein bisschen aufwändiger und sollte daher Schritt für Schritt angegangen werden. Das Ziel ist klar; Ein Aufruf sollte folgendermaßen aussehen:
3 EINTRAG
Damit soll die '3' in der zweiten Zeile an der Stelle eintragen werden, wo in der ersten Zeile ebenfalls eine '3' steht, oder, wenn die nicht gefunden wird, in der ersten Spalte, bei der in der ersten Zeile eine Null steht, also:
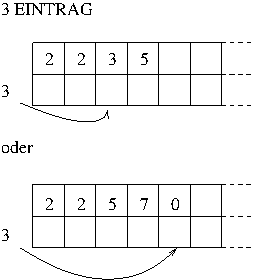
Machen wir es Schritt für Schritt und wie wir es mittlerweile von
Forth gewohnt sind 'von hinten'. Irgendwo, ganz tief in der Routine,
die wir nun brauchen, müssen die beiden Spaltenwerte getestet
werden, der aus der ersten Zeile daraufhin, ob er Null ist und die
beiden, ob sie gleich sind. In jedem Fall soll ein Flag zurück
gegeben werden, das 'wahr' ist, sonst ein Flag, dass 'falsch' ist.
Da wir zwei Tests haben, muss noch ein neues Wort vorgestellt werden
OR. Dieses Wort nimmt zwei Werte vom Stack und führt
eine bitweise Oder-Operation mit ihnen durch. Wenn sie nicht wissen,
was das ist, ist das nicht so schlimm, später wird es erklärt
werden, hier reicht es zu wissen, dass diese Operation ein 'wahr'
auf dem Stack hinterlässt, wenn eine oder beide Zahlen auf dem Stack
'wahr' waren, sonst ein 'falsch'.
: TEST-WERt ( n2 n1 -- f )
DUP 0=
ROT ROT
=
OR ;
Gehen wir das Wort mal durch. Zu Beginn sieht der Stack folgendermaßen aus:
| Wert aus 1. Zeile |
| Einzutragender Wert |
Zuerst wird der oberste Wert auf Null getestet, da er später noch gebraucht wird, wird er erst verdoppelt. Nach diesem Test sieht der Stack folgendermaßen aus:
| Ergebnis Nulltest |
| Wert aus 1. Zeile |
| Einzutragender Wert |
Nach dem doppelten ROT liegen die beiden zu
vergleichenden Werte wieder oben auf dem Stack und zwar in der Form:
| Wert aus 1. Zeile |
| Einzutragender Wert |
| Ergebnis Nulltest |
Das = testet nun die beiden oben liegenden Werte auf
Gleichheit, so dass auf dem Stack nun nur noch die beiden
Testergebnisse in Form von Flags liegen. Die werden abschließend mit
einem OR zu einem Flag zusammengefasst.
Nun muss nur noch dafür gesorgt werden, dass der Wert aus der 1. Zeile oben und der Wert einzutragende Wert darunter liegt. Dazu soll ein Wort her, das auf dem Stack (unten) den einzutragenden Wert und oben die Adresse einer Spalte (2. Zeile) übergeben bekommt und die Werte in gewünschter Form liefert.
: TEST-SPALTE ( n addr -- f )
OVER OVER 4 - @ TEST-WERT ;
Und damit ist die Sache dann fast schon fertig. Nun brauchen wir nur
noch ein Wort, das so lange durch die Tabelle läuft, bis die
richtige Spalte gefunden wurde und dort den Wert einträgt. Die
Adresse läuft dabei durch die 2. Zeile. Nur Spalten bei denen da
eine Null liegt, kommen überhaupt in Frage. Beim Erhöhen der Adresse
muss man daran denken, dass auf jeden Fall erhöht wird, daher muss
die Adresse erst einmal auf die nächste Spalte gesetzt werden. Das
NAECHSTE0 dient nur dazu weiter zu rücken, wenn da
schon was steht.
: EINTRAG ( n -- )
0 PRIMFAKTOREN 4 +
NAECHSTE0
BEGIN
TESTE-SPALTE
IF
! -1
ELSE
8 + NAECHSTE0 0
THEN
UNTIL ;
Zähler und Nenner können in Primfaktoren zerlegt werden und die
Routinen, um diese in die Tabelle einzufügen sind auch schon fertig.
Bisher haben wir die Primfaktoren allerdings ausgegeben. Das ist nun
nicht mehr sinnvoll, denn sie sollen ja in die Tabelle eingetragen
werden. Besser ist es daher das Wort PRIMF so
abzuändern, dass nur der nächste Primfaktor und der Divisionsrest
zurück gegeben werden. Das ist allerdings einfach, die neue
Definition von PRIMF lautet nun:
: PRIMF 2 BEGIN SWAP OVER ?HAT-TEILER IF SWAP -1 ELSE SWAP 1+ 0 THEN UNTIL ;
Es wird eigentlich nur die Abbruchbedingung geändert. Dieses Wort endet dann, wenn ein Primfaktor gefunden wurde. Auf dem Stack liegen nach dem Wort oben der Primfaktor und darunter der Divisionsrest.
Mit dieser Neudefinition von PRIMF können nun endlich
Zähler und Nenner in die Tabelle eingetragen werden. Dazu müssen die
Primfaktoren der ersten Zahl in die Tabelle gefüllt werden und die
der zweiten Zahl in die Tabelle eingetragen werden. Die Stuktur des
Wortes ist eigentlich sehr einfach:
: IN-TABELLE
BEGIN
PRIMF FUELL
DUP
1 =
UNTIL
DROP
BEGIN
PRIMF EINTRAG
DUP
1 =
UNTIL DROP ;
Nun kann der ggT der beiden Zahlen berechnet werden. Dazu muss die
Tabelle durchlaufen werden. Sind die Zahlen in beiden Zeilen gleich,
dann werden sie zum ggT multipliziert, wenn sie nicht beide Null
sind. Letzteres ist das Abbruchkriterium der Schleife. Hier bietet
sich wieder eine BEGIN ... WHILE ... REPEAT-Schleife
an, aber der Reihe nach.
Zu Beginn wird eine Eins als Startwert für den ggT und die Adresse der ersten Spalte auf den Stack gelegt. Dann beginnt die Schleife:
: GGT
1 0 PRIMFAKTOREN
BEGIN
An der Adresse müssen nun beide Einträge geholt werden. Dazu wird
die Adresse verdoppelt, weil sie beim Auslesen verloren geht und
dann ein neues Wort verwendet: 2@. Dieses Wort holt
nicht nur einen Wert auf den Stack, sondern zwei, die nacheinander
im Speicher liegen. Auf diese Art werden beide Zeilenwerte
gleichzeitig auf den Stack gelegt. Nun muss getestet werden, ob
beide Null sind. Das geschieht durch das Logik-Wort
OR, den wir ja schon verwendet haben. Ist einer der
beiden Werte nicht Null, dann ist auch das Ergebnis nicht Null. Da
WHILE die Schleife beendet, sobald hier eine Null
auftaucht brauchen wir nichts weiter zu machen.
DUP 2@ OR
WHILE
Waren nicht beide Werte Null, dann muss getestet werden, ob
eventuell einer Null ist. Dazu müssen sie aber erst wieder geholt
werden. Hier kommt dann ein neues Wort ins Spiel. Das Wort
AND ist die logische Und-Verknüpfung und ich vertröste
wieder auf später. Es reicht hier zu wissen, dass sie dann
nicht-Null ist, wenn beide Werte nicht Null sind.
DUP 2@ AND
Nach dem Test muss geprüft werden, ob die Verknüpfung nicht Null ergeben hat, die beiden Werte also gleich waren. In dem Fall muss der vorläufige ggT mit dem Wert multipliziert werden. Dazu muss er noch einmal geholt werden.
IF
DUP @ ROT * SWAP
THEN
Abschließend muss nur noch die Adresse auf die nächste Spalte erhöht werden.
8 +
Ist die Schleife durchlaufen, dann muss nur noch die Adresse vom Stack genommen werden. Das Ganze sieht dann so aus:
: GGT
1 0 PRIMFAKTOREN
BEGIN
DUP 2@ OR
WHILE
DUP 2@ AND
IF
DUP @ ROT * SWAP
THEN
8 +
REPEAT
DROP ;
Das Kapitel neigt sich endgültig seinem Ende. Wenn sie bis hierhin alles verstanden haben, dann dürfte das nun kein Problem mehr sein:
: TEL ( n n -- )
LEER
2DUP
IN-TABELLE
GGT
DUP ROT SWAP /
ROT ROT /
61 EMIT . 47 EMIT . ;
Probieren sie es aus, es funktioniert. Mir ist klar, dass diese hier definierten Worte nicht optimal sind und das in zweierlei Hinsicht: Zum einen wird nicht auf mögliche Fehlersituationen reagiert, zum anderen da der Kode wirklich nicht effektiv und kompakt ist, wie er eigentlich sein sollte. Bevor es in den nächsten Kapiteln dann zu den Einzelheiten von Forth geht, hier noch mal der Kode im Überblick:
: ?HAT-TEILER ( Zahl Teiler -- Zahl/Quotient Teiler Flag )
OVER SWAP /MOD OVER IF DROP ELSE ROT DROP SWAP THEN 0= ;
: PRIMF ( Zahl -- Primfaktor )
2 BEGIN
SWAP OVER ?HAT-TEILER IF SWAP -1 ELSE SWAP 1+ 0 THEN
UNTIL ;
: MACH-TABELLE CREATE 8 * ALLOT DOES> SWAP 8 * + ;
50 MACH-TABELLE PRIMFAKTOREN
: LEER 0 PRIMFAKTOREN 50 8 * 0 FILL ;
: NAECHSTE0 BEGIN DUP @ WHILE 8 + REPEAT ;
: FUELL 0 PRIMFAKTOREN NAECHSTE0 ! ;
: TEST-WERT ( n1 n1 - f )
DUP 0= ROT ROT = OR ;
: TEST-SPALTE ( n addr -- n addr f )
OVER OVER 4 - @ TEST-WERT ;
: EINTRAG ( n -- )
0 PRIMFAKTOREN 4 +
NAECHSTE0
BEGIN
TEST-SPALTE
IF
! -1
ELSE
8 + NAECHSTE0 0
THEN
UNTIL ;
: IN-TABELLE
BEGIN PRIMF FUELL DUP 1 = UNTIL
DROP
BEGIN PRIMF EINTRAG DUP 1 = UNTIL DROP ;
: GGT ( -- n )
1 0 PRIMFAKTOREN
BEGIN
DUP 2@ OR
WHILE
DUP 2@ AND
IF
DUP @ ROT * SWAP
THEN
8 +
REPEAT
DROP ;
: TEL ( n n -- )
LEER 2DUP IN-TABELLE
GGT
DUP ROT SWAP /
ROT ROT /
61 EMIT . 47 EMIT . ;